Problematics | The truth about lying

A book of puzzles I recently consulted contains an elementary version of a puzzle that has appeared in Problematics earlier (Puzzle #70.1, January 1, 2024). Since you have already the tougher version, there is no point trying the simpler one now. The reason for bringing this up, however, is that I think the solution printed in the book is wrong.

It runs like this: In a group of people, some always speak the truth and some always lie. Four of them sit in a circle. To each one, we ask: “Is the person on your left truthful or a liar?” Each one replies: “A liar!” The puzzle is to determine which ones are truthful and which ones are liars, and the book concludes that the first and third are truthful and the other two are liars. I think, however, that the puzzle is indeterminate. With an even number of people, all we can conclude is that the truth-tellers and liars are sitting alternately. So, either the first and third are truthful and the other two are liars, or the first and third and liars are liars and the other two are truthful. Please let me know if there is anything I have missed here.

Onward to our next puzzle, which is again about people who always lie and others who never do.

#Puzzle 98.1

Meet a group of five people, each of whom either always tells the truth or always lies. We do not know how many of the five are truthful and how many are liars, but both kinds exist in the group.

To find out, you ask one of them: “Are you truthful?”

“Yes,” she replies.

It was a wasted question, of course. So you ask the second person: “How many of you are truthful?”

“Two, including myself,” he replies.

Another man butts in: “There are three liars among us.”

Glad to be making progress, you turn to the fourth person, a woman. “Does this group include more liars or more truthful persons?”

“The liars outnumber the truthful,” she mourns.

“She lies,” says the fifth, also a woman. “The truthful outnumber the liars.”

Who is what?

#Puzzle 98.2

A magician turns his back and asks a member of his audience to roll three dice. He proceeds to give the following instructions:

1. Double the number on the first die and add 5.

2. Multiply the sum by 5.

3. To this total add the number of the second die.

4. Multiply the new total by 10.

5. Add the number on the third die and tell me the grand total.

The moment the spectator gives the total, the magician announces the number on each die.

How is it done?

MAILBOX: LAST WEEK’S SOLVERS

#Puzzle 97.1

Hi Kabir,

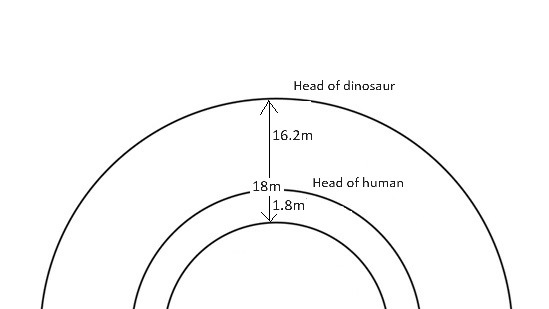
Hope I understood the problem correctly. Treating it as a set of concentric circles, the difference between the distance travelled by the head of the dinosaur and the distance travelled by the head of the human is equal to the difference between the circumferences of the respective circles. So the extra distance travelled by the dinosaur’s head is 2π(18 – 1.8) = 2π x 16.2 = 101.78m. One doesn’t need the circumference of the Earth to calculate this.

— Dr Sunita Gupta, Delhi

#Puzzle 97.2

Hi Kabir,

a² – b² = x³

a³ – b³ = y²

The smallest values of a and b satisfying the above integer equations are 10 and 6.

10² – 6² = 64 = 4³

10³ – 6³ = 784 = 28²

This could be found manually by exploring the values in the range 1 to 10 using just an Excel spreadsheet. Interestingly, the next higher pair of values is 640 and 384. This, of course, required a program to explore.

640² – 384² = 262144 = 64³

640³ – 384³ = 205520896 = 14336²

In retrospect, it can be seen that this pair of values can be obtained by multiplying the earlier pair by 64, the smallest integer (greater than 1) that is both a perfect square and a perfect cube. This observation implies the existence of infinitely many solutions.

— Professor Anshul Kumar, Delhi

***

The smallest numbers satisfying the equations would be a = 10 and b = 6. This is assuming that a value of 0 is not acceptable. If it is ok, the values a = 1 and b = 0 would also satisfy the conditions.

— Kanwarjit Singh, Chief Commissioner of Income-Tax (retired)

Strictly speaking, a value of 0 should not have been acceptable. But since this was not specified in the original puzzle, I am accepting the solution (1, 0) from a couple of readers who did not mention (10, 6).

Solved both puzzles: Dr Sunita Gupta (Delhi), Professor Anshul Kumar (Delhi), Kanwarjit Singh (Chief Commissioner of Income-Tax, retired), Sanjay S (Coimbatore), Avanti Kashikar (Mumbai), YK Munjal (Delhi), Akshay Bakhai (Mumbai), Harshit Arora (IIT Delhi), Sampath Kumar V (Coimbatore), Yadvendra Somra (Sonipat), Ajay Ashok (Mumbai)

Solved #Puzzle 97.2: Shishir Gupta (Indore)

Problematics will be back next week. Please send in your replies by Friday noon to problematics@hindustantimes.com.